DM Seminar
Семинар 22 августа 2002 года
Четверг, 22 августа, комната 106. Начало в 18:00.
Докладчик: В. Крейнович (University of Texas at El Paso).
FUZZY LOGIC FROM THE MATHEMATICIAN'S VIEWPOINT: WHAT IS IT? WHAT ARE ITS MAIN RESULTS? MAIN SUCCESSES? MAIN PROBLEMS?Fuzzy logic is a (successful) way to transform the expert's knowledge of the type "if the velocity is big and the distance from the object is small, hit the brakes and decelerate as fast as possible" into an actual control. To apply this transformation one must: 1) describe how to formalize words like "small", "big"; 2) choose operations corresponding to "and" and "or"; 3) choose a method that transforms the resulting fuzzy variable into a single value. The wrong choice can drastically affect the quality of the resulting control, so the problem of choosing the right procedure is very important. From mathematical viewpoint these choice problems correspond to non-linear optimization and are therefore extremely difficult. We describe how the corresponding optimization problem can be solved, what are the resulting choices, what logics they correspond to, and what are the remaining open problems.
Семинар 24 июня 2002 года
Понедельник, 24 июня, комната 203. Начало в 14:00.
Докладчик: Д. В. Пасечник (Франкфурт).
FINDING OPTIMUM SUBJECT TO FEW QUADRATIC CONSTRAINTS IN POLYNOMIAL TIME (joint work with D.Grigoriev i E. de Klerk)It is shown that quadratic programming in
 variables subject to
variables subject to 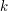 quadratic constraints has time complexity
quadratic constraints has time complexity 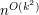 , while feasibility can be tested in
, while feasibility can be tested in 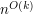 operations. The described procedure outputs the optimal value, as well as an optimal point, if they exist. Otherwise, it reports the range of the objective function on the feasible region. Optimal points and values are given exactly, via algebraic numbers. For this purpose the tools of quantifier elimination over the real closed fields with infinitesimals are involved.
operations. The described procedure outputs the optimal value, as well as an optimal point, if they exist. Otherwise, it reports the range of the objective function on the feasible region. Optimal points and values are given exactly, via algebraic numbers. For this purpose the tools of quantifier elimination over the real closed fields with infinitesimals are involved.In contrast, the best previously known procedure needs
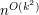 operations just for answering feasibility in the homogeneous case due to A.Barvinok, and no polynomial-time procedure previously known is able to find a feasible point with prescribed precision.
operations just for answering feasibility in the homogeneous case due to A.Barvinok, and no polynomial-time procedure previously known is able to find a feasible point with prescribed precision.
Семинар 21 июня 2002 года
Пятница, 21 июня, комната 106. Начало в 18:00.
Докладчик: А. Кожевников.
Доклад по статье P.ParriloИСПОЛЬЗОВАНИЕ ПОЛУОПРЕДЕЛЕННОГО ПРОГРАММИРОВАНИЯ ДЛЯ ПОИСКА ПОЛУАЛГЕБРАИЧЕСКИХ ДОКАЗАТЕЛЬСТВ
Полуалгебраические системы доказательств -- один из новых интересных и активно изучаемых классов систем пропозициональных доказательств. В статье описывается новый подход для определения разрешимости системы полиномиальных неравенств с использованием полуопределенного программирования.
Основная идея метода заключается в переформулировке задачи разложения полинома от многих переменных в сумму квадратов в полуопределенную программу. Также используются некоторые результаты из вещественной алгебраической геометрии.
Автором статьи предложен эффективный алгоритм нахождения доказательства ограниченной степени в Positivstellensatz. Методы, использованные в этом алгоритме, имеют приложение и к другим задачам.
Источник: P.Parrilo, "Semidefinite programming relaxations for semialgebraic problems", Preprint, 2001, 15.
Семинар 18 июня 2002 года
Вторник, 18 июня, комната 412. Начало в 15:00.
Докладчик: Б. Ю. Конев.
СУБЪЕКТИВНЫЙ ВЗГЛЯД НА СИСТЕМЫ АВТОМАТИЧЕСКОГО ВЫВОДА ТЕОРЕМСеминар 11 июня 2002 года
Вторник, 11 июня, комната 106. Начало в 18:00.
Докладчик: А. О. Слисенко (Paris).
РАЗРЕШИМЫЕ КЛАССЫ В ЛОГИКЕ, ОСНОВАННЫЕ НА КОНЕЧНОЙ ОПРОВЕРЖИМОСТИ И ВЫПОЛНИМОСТИСеминар 26 апреля 2002 года
Пятница, 26 апреля, комната 106. Начало в 18:00.
Докладчик: А. Кожевников.
Доклад по статье A.Atserias, M.BonetОБ АВТОМАТИЗАЦИИ МЕТОДА РЕЗОЛЮЦИЙ И СВЯЗАННЫХ С НЕЙ СИСТЕМ ДОКАЗАТЕЛЬСТВ
(продолжение)
Семинар 19 апреля 2002 года
Пятница, 19 апреля, комната 106. Начало в 18:00.
Докладчик: А. Кожевников.
Доклад по статье A.Atserias, M.BonetОБ АВТОМАТИЗАЦИИ МЕТОДА РЕЗОЛЮЦИЙ И СВЯЗАННЫХ С НЕЙ СИСТЕМ ДОКАЗАТЕЛЬСТВ
Создания эффективного алгоритма для доказательства тавтологичности -- одна из важнейших задач информатики. В статье описывается новый алгоритм для доказательств тавтологичности методом резолюций, основанный на системах доказательств Res(k), являющихся обобщениями метода резолюций. Доказывается, что полученный алгоритм не хуже других алгоритмов для метода резолюций, а во многих случаях экспоненциально лучше.
Также в этой статье исследуется "слабая автоматизируемость" резолюционной системы доказательств, то есть, являются ли автоматизируемыми системы, полиноминально моделирующие метод резолюций. Эта проблема сводится к вопросу о существовании интерполянтов в системе доказательств Res(2).
В качестве побочного результата построен новый класс тавтологий, имеющих короткие доказательства методом резолюций, но обладающих при этим большой "шириной". Таким образом, снимается вопрос Алехновича и Разборова об автоматизации метода резолюций за квазиполиномиальное время.
Источник: A.Atserias, M.Bonet, "On the Automatizability of Resolution and Related Propositional Proof Systems", ECCC TR02-010.
Семинар 5 апреля 2002 года
Пятница, 5 апреля, комната 106. Начало в 18:00.
Докладчик: Ю. Лифшиц.
СВЯЗЬ КОНЕЧНЫХ АВТОМАТОВ С РЕГУЛЯРНЫМИ ВЫРАЖЕНИЯМИ ЗАДАЧА ОБ УНИВЕРСАЛЬНОМ ГРАФЕЭта задача возникла в теории конечных автоматов. Известно, что для языка каждого регулярного выражения существует конечный автомат, который этот язык распознает. При попытке дать нижнюю оценку количества переходов в этом автомате Hagenah и Muscholl сформулировали следущий результат:
Количество переходов в конечном недетерминированном автомате без пустых переходов, который распознает регулярный язык из
 букв -- не меньше, чем количество ребер в Универсальном графе (УГ).
букв -- не меньше, чем количество ребер в Универсальном графе (УГ).В той же статье получена и верхняя оценка:
Для любого регулярного выражения, построенного за
 шагов, можно построить недетерминированный конечный автомат без пустых переходов, который будет распознавать язык этого выражения и содержать не более чем
шагов, можно построить недетерминированный конечный автомат без пустых переходов, который будет распознавать язык этого выражения и содержать не более чем 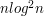 переходов.
переходов.Таким образом, цель настоящей работы -- получить нижнюю оценку на количество ребер в УГ. Оценка, полученная в работе Hagenah и Muscholl --
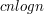 . Результат настоящей работы -- нижняя оценка
. Результат настоящей работы -- нижняя оценка 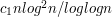 . Основная идея доказательства -- переход от ориентированного графа к стрелочным структурам. Однако, по мнению автора, таким путем невозможно получить оценку
. Основная идея доказательства -- переход от ориентированного графа к стрелочным структурам. Однако, по мнению автора, таким путем невозможно получить оценку 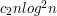 .
.
Семинар 15 марта 2002 года
Пятница, 15 марта, комната 106. Начало в 18:00.
Докладчик: Б. Ф. Мельников (Ульяновский гос.университет).
ПРОСТОЕ РЕШЕНИЕ ПРОБЛЕМЫ ЗВЕЗДНОЙ ВЫСОТЫ (Часть I)Проблема звездной высоты регулярного языка была поставлена в самом начале 1960-х годов и очень долгое время оставалась нерешенной. Кратко сама проблема может быть сформулирована следующим образом: определяем звездную высоту (ЗВ) регулярного выражения (РВ) как максимальное вложение в нем операции "звезда"; известно, что для каждого регулярного языка (РЯ) существует бесконечно много РВ, определяющих этот язык; существует ли алгоритм, определяющий, какое именно из этих РВ имеет минимальную ЗВ? В 1987-м году вышла пока единственная публикация с довольно сложным алгоритмом, решающим данную проблему (K.Hashiguchi).
Автор данных тезисов предлагает значительно более простое решение, базирующееся на построении специальных недетерминированных конечных автоматов (КА). Данное решение является продолжением серии работ автора, связанных с исследованием РЯ с помощью т.н. функций разметки состояний КА; в тех работах, среди прочих, были решены задачи минимизации КА по другим критериям - вершинной и дуговой.
Вторая часть доклада состоится на заседании семинара лаборатории математической логики ПОМИ в понедельник, 18 марта в 14:00, к.203.
Семинар 1 марта 2002 года
Пятница, 1 марта, комната 106. Начало в 18:00.
Докладчик: Э. Гирш (совместная работа с Д.Григорьевым и Д.Пасечником).
ПОЛУАЛГЕБРАИЧЕСКИЕ ДОКАЗАТЕЛЬСТВАВывод пропозициональной тавтологии в полуалгебраической системе доказательств заключается в опровержении некоторой системы полиномиальных неравенств. Эти системы являются довольно сильными: в них имеются короткие доказательства принципа Дирихле, Цейтинских тавтологий, нераскрашиваемости k-клики в (k-1) цвет и т.д. Тем не менее, для наиболее слабых из полуалгебраических систем получены экспоненциальные нижние оценки на длину вывода.

