Студенческий конкурс решения задач
2001-2002 гг.
Задача 10. Минимизация функционала.
Для каждого 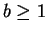 через
через 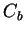 обозначим множество
всех функций
обозначим множество
всех функций ![$f\in C[0,1]$](img3.png) , для которых
, для которых
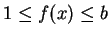 при всех
при всех
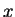 из
из ![$[0,1]$](img6.png) . Пусть
. Пусть
(А) Для каждого 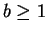 найдите оценки сверху и/или снизу для
найдите оценки сверху и/или снизу для
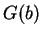 .
.
(Б) Найдите точное значение 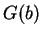 .
.
Назад к списку задач
![]() через
через ![]() обозначим множество
всех функций
обозначим множество
всех функций ![]() , для которых
, для которых
![]() при всех
при всех
![]() из
из ![]() . Пусть
. Пусть
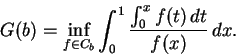
![]() .
.