Студенческий конкурс решения задач
2001-2002 гг.
Задача 2. Корни комплексного многочлена и его
производной.
Пусть 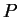 -- многочлен с комплексными коэффициентами
степени
-- многочлен с комплексными коэффициентами
степени 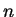 и
и
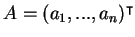 -- вектор-столбец,
состоящий из его корней (в произвольном порядке). Построим новый
вектор
-- вектор-столбец,
состоящий из его корней (в произвольном порядке). Построим новый
вектор
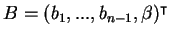 , где
, где 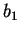 , ...,
, ...,
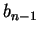 -- корни производной
-- корни производной 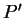 а
а
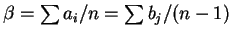 . Известно, что для любого многочлена корни производной
лежат в выпуклой оболочке корней самого многочлена. Поэтому
существует такая стохастическая матрица
. Известно, что для любого многочлена корни производной
лежат в выпуклой оболочке корней самого многочлена. Поэтому
существует такая стохастическая матрица 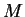 (т.е. матрица из
вещественных неотрицательных чисел с суммами по строкам, равными
1), что ее последняя строка есть
(т.е. матрица из
вещественных неотрицательных чисел с суммами по строкам, равными
1), что ее последняя строка есть
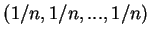 и
и 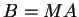 .
Докажите, что матрицу
.
Докажите, что матрицу 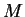 можно выбрать дважды-стохастической,
т. е. с суммами по столбцам, также равными 1:
можно выбрать дважды-стохастической,
т. е. с суммами по столбцам, также равными 1:
(А) для 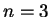 ;
;
(Б) для 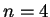 ;
;
(В) для произвольного 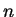 .
.
Назад к списку задач
![]() ;
;
![]() ;
;
![]() .
.