Студенческий конкурс решения задач
2001-2002 гг.
Задача 3. Плоская проекция набора
скрещивающихся прямых.
Дана матрица 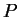 размера
размера 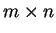 , состоящая из нулей и единиц.
Найти необходимые и/или достаточные условия, при которых
существует набор прямых
, состоящая из нулей и единиц.
Найти необходимые и/или достаточные условия, при которых
существует набор прямых 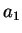 , ...,
, ..., 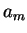 ,
, 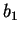 , ...,
, ..., 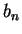 в
пространстве
в
пространстве 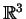 , проекции которых на плоскость
, проекции которых на плоскость 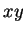 суть
соответственно прямые
суть
соответственно прямые 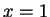 , ...,
, ..., 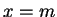 ,
, 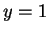 , ...,
, ..., 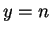 , причем
над точкой
, причем
над точкой 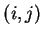 прямая
прямая 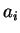 выше прямой
выше прямой 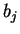 , если
, если
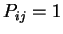 , и ниже, если
, и ниже, если 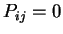 .
.
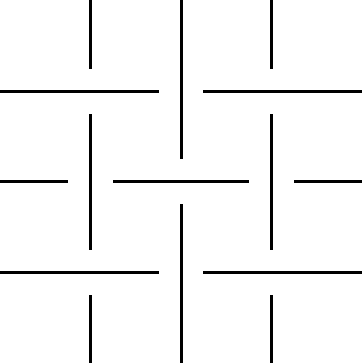
На рисунке приведена геометрическая иллюстрация для матрицы
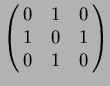 .
.
Назад к списку задач
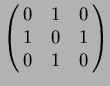 .
.
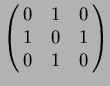 .
.
