Студенческий конкурс решения задач
2001-2002 гг.
Задача 5. Вполне унимодальные псевдо-булевы функции.

Псевдо-булева функция (ПБФ) $n$ переменных -- это нумерация вершин $n$-мерного куба, т.е. взаимно-однозначное отображение $\{0,1\}^n \to \{1,2,\dots,2^n\}$. Назовем ПБФ вполне унимодальной, если она имеет единственный локальный минимум на каждой двумерной грани куба. (Например, функция, принимающая в последовательных вершинах квадрата значения 1234, этим свойством обладает, а функция 1324 -- нет: для нее 1 и 2 являются двумя локальными минимумами). На рисунке приведен пример вполне унимодальной ПБФ размерности 3:

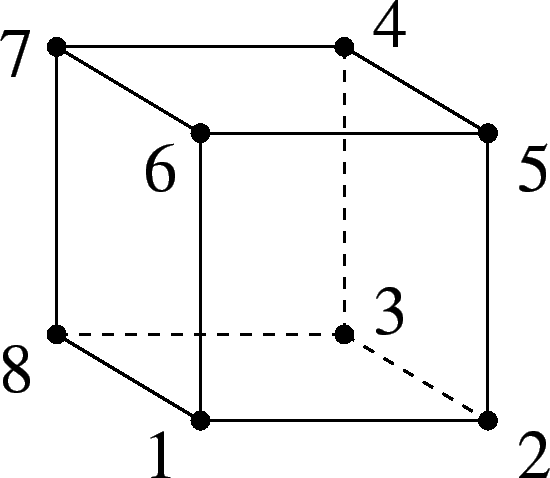
\epsfbox{PBF.eps}

(А) Найдите число вполне унимодальных псевдобулевых функций $b_n$ для малых значений размерности (скажем, $n=3,4,5$).

(Б) Найдите асимптотику (или какие-то -- верхние/нижние -- асимптотические оценки) для числа $b_n$ при $n\to\infty$.

В обоих случаях разрешается вести подсчет с учетом или без учета симметрии куба; если симметрии учитываются, то используемую группу следует явно описать.



Назад к списку задач