(А) Разложите на множители над
![]() (
(![]() --
нечетное простое) многочлен
--
нечетное простое) многочлен
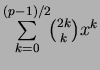 .
.
(Б) Пусть ![]() -- простое,
-- простое,
![]() . Докажите, что
многочлен
. Докажите, что
многочлен
Задача 7. Многочлены над конечными полями.
(А) Разложите на множители над
(Б) Пусть ![]() (
(![]() --
нечетное простое) многочлен
--
нечетное простое) многочлен
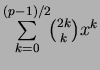 .
.
![]() -- простое,
-- простое,
![]() . Докажите, что
многочлен
. Докажите, что
многочлен
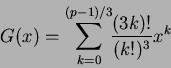
(В) Верно ли, что ![]() раскладывается на квадратичные множители
над
раскладывается на квадратичные множители
над
![]() ?
?