Напомним, что
![]() - группа матриц
второго порядка с целыми элементами и определителем
- группа матриц
второго порядка с целыми элементами и определителем ![]() .
Матрица
.
Матрица
![]() называется примитивной,
если не существует
называется примитивной,
если не существует ![]() и матрицы
и матрицы
![]() таких, что
таких, что ![]() .
.
(А) Проверьте, будут ли следующие матрицы примитивными:
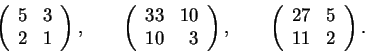
(Б) Найдите какие-либо достаточные и/или необходимые условия примитивности.